Démonstrations : téléchargeables dans la rubrique Démonstrations et outils.

Objectif du projet de recherche

Ce problème mathématique consiste en la résolution de l’équation ci-dessous :

où les Ai sont les inconnues à trouver et les Ti sont ces valeurs théoriques à chercher. A chaque pas on présente à l’entrée du système un vecteur X dont la composante Xi est associée à l’inconnue Ai. Le système calcule la sommation compte-tenu des valeurs courantes qu’il possède et on lui indique si son résultat est supérieur, inférieur ou égal à la somme théorique qu’il aurait dû indiquer. De ce feed-back, le système modifie les valeurs des coefficients selon ses critères internes.

Dans ce cas précis, les entrées Xi sont tirées uniformément dans une plage de valeurs [-100, +100] et les Ti sont choisis aléatoirement dans l’intervalle [1, +1000].

Les agents de calcul

L’identification des agents est assez évidente dans la mesure où ce qui doit s’adapter au cours du temps et pour lequel nous n’avons pas de fonction précise à la conception sont les inconnues de l’équation. Ces agents vont avoir trois comportements possibles au cours du temps : augmenter leur valeur courante, la diminuer ou ne pas la modifier.

Les valeurs initiales des agents sont déterminées aléatoirement dans la plage des valeurs possibles. A chaque exemple d’entrée tous les agents pourraient modifier leur valeur courante pour que la somme globale réduise l’écart indiqué par le feed-back. Mais il sont ainsi tous en situation de concurrence selon la théorie des Amas. Ils vont donc chercher à modifier en fonction de leur "motivation" respective.

Résultats et analyse

La visualisation de la résolution est indiquée dans la figure suivante.

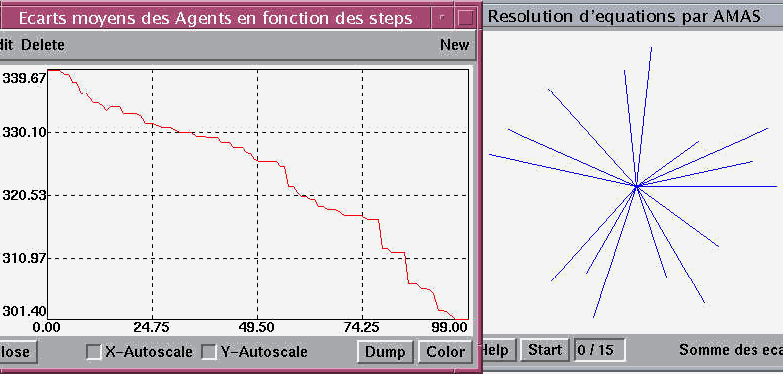
Interface

Dans la partie gauche nous voyons la distance moyenne de l’ensemble des inconnues au fur et à mesure des essais. Cette distance décroît régulièrement pour être égale à zéro lorsque la solution est trouvée pour l’ensemble des inconnues. Dans la partie droite chaque segment représente la distance à sa solution. Visuellement, toutes les solutions (en réalité indépendantes) sont représentées en un point focal au centre. Lorsque la solution est trouvée, il ne reste plus qu’un point central dans la fenêtre.

Les caractéristiques de cette méthode ont été explorées statistiquement par de nombreuses expériences jusqu’à 100 inconnues.

C’est ce qui est représenté dans le graphique suivant. Par exemple la solution est trouvée en moyenne en moins de 2000 essais lorsqu’il s’agit de trouver 10 inconnues. Pour 100 inconnues, il faut environ 18000 tentatives.

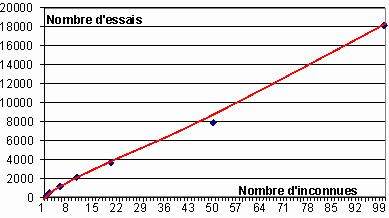
Courbe résultat / Results curve

La question était de savoir s’il existait une théorie mathématique à même de résoudre ce genre de problème, ce qui nous permettrait d’avoir un critère de comparaison : il s’agit de la programmation linéaire en nombre entier. Pour cette technique de résolution sous contraintes, il faut statistiquement environ 600 000 essais pour qu’elle trouve la solution avec 10 inconnues. De plus, nous avons expérimentalement noté qu’au delà d’un espace de recherche de 10¹² la programmation linéaire ne résolvait plus l’équation car l’espace mémoire disponible était saturé.

De notre côté la théorie des AMAS a surtout été explorée pour 100 inconnues, même si nous avons vérifié que le système résout les équations avec 1000 inconnues. Pour 100 inconnues, l’espace de recherche est de l’ordre de 10³⁰⁰, ce qui est bien au-delà de ce que peut faire la programmation linéaire et avec un nombre d’essais sans commune mesure.